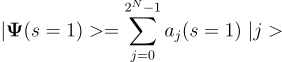OK so I realized when I was writing up the game description that I really should split this part out into a separate thing. I swear the next one will be the game! I’ll try to make this entertaining to make up for teasing it for so long!

There are few subjects that are as profound and fascinating as quantum physics.

Admittedly, it’s a bit weird and some parts of it are hard to understand. But I’m going to try to walk you through the bits that are necessary for understanding my approach to trying to make quantum computers useful.

And even better, parts of a new type of quantum-assisted game-playing AI!

Let’s Start With The Schrödinger Equation

You’ve probably heard of the Schrödinger Equation. But what is it? Here’s a description from the wikipedia article:

Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of the wavefunction, the quantum-mechanical characterization of an isolated physical system.

There’s a only a small number of things we need to know to parse this, and none of them is super hard to understand.

What’s a Wavefunction?

Let’s say we have a collection of N objects, each of which can have two states (like +1 or -1 … sound familiar?). Furthermore, let’s assume that these N objects are qubits (quantum bits), which are two-state objects just like we’ve been working with, but for some reason they obey the laws of quantum mechanics instead of classical physics. We’re going to assume these N objects are very well isolated from the rest of the Universe (like in a really quiet cat-sized box).

How many possible states are there for our N objects? There are 2ᴺ — every configuration from all N objects being in the -1 state, to all N being in the +1 state. For example, let’s say we had N=3. Then the number of configurations is 2³=8, and if we wrote them all down we’d have [-1,-1,-1], [-1,-1,1], [-1,1,-1], [-1,1,1], [1,-1,-1], [1,-1,1], [1,1,-1], and [1,1,1].

In quantum mechanics there’s a very useful notation for writing down all the allowed states of a system, called bra-ket notation. It looks scary if you haven’t seen it before, but don’t be alarmed! It’s just a book-keeping thing.

OK you see those 2³=8 states we wrote down just now? We wrote them down in a particular order, just like you’d write down ascending binary numbers if you swapped -1 for 0. If we pretended each state was a binary number, the list would go from 0 to 2ᴺ-1 (written in binary). Let’s then write each of the states like this | j >, where the | > thing is called a ‘ket’, and the j is the state whose binary representation is just the number j. For the example above, the list of measured variables [-1, 1, 1] would correspond to binary 011 which is 4, and we’d represent this state in the bra-ket notation as | 4 >.

The wavefunction, which I’ll denote | Ψ(t) >, is a vector of complex numbers of length 2ᴺ. Each entry in this vector corresponds to one of the possible configurations of the N objects’ states, like the eight states I wrote down above. We can write the wavefunction down like this:

which means ‘the wavefunction is a sum over all possible 2ᴺ states an N-object system could be in (that’s the | j > terms), where each possible state | j > is multiplied by a number that is a function of time aⱼ(t)’. The aⱼ(t) are complex numbers called probability amplitudes. If the jth probability amplitude is aⱼ(t), then the probability of the system being in state | j > at time t is |aⱼ(t)|².

The wavefunction is defined so that the sum over all |aⱼ(t)|² is equal to one at all times, to make sure that these are in fact probabilities.

This is what a wavefunction is and does — it stores the numbers aⱼ(t) that we can use to compute the probabilities |aⱼ(t)|² of being in all of the possible states the system could be in at any time.

This might sound dry and boring, but if quantum mechanics is a good description of our Universe, then even the Universe itself has a wavefunction, and the aⱼ(t) for that wavefunction encode every single thing that not only did happen in our branch of the wavefunction, but every single thing that could ever happen.

You feeling hungry, or sad, or stabby today? That’s all caused by, and in, the aⱼ(t) of the wavefunction of the Universe.

Here’s a mind-blower: not only are all those things in it, but all possible paths throughout history are in it. Every single possible consistent history our universe could have taken is contained in those numbers. Why this is is a whole other post — let’s leave it for a future conversation over beers.

What’s a Hamiltonian?

The second thing I need to introduce is a matrix called the Hamiltonian, denoted H(t), which in our case will also be a function of time. A matrix is just a table of numbers that have rows and columns. It must have the property that H*ᵢⱼ = Hⱼᵢ, where the star means take the complex conjugate (put a minus sign in front of all the imaginary terms — by the way if you want an awesome description of all this beyond my Coles notes, see section 8.5 of this). The reason for this restriction on the Hamiltonian is that it’s necessary so that the |aⱼ(t)|² can be interpreted as probabilities.

The allowed energies of the system are given by the eigenvalues of this matrix. Its size scales exponentially with the number of qubits being modeled — if a physical system has N qubits, then the Hamiltonian is a matrix of size 2ᴺx2ᴺ.

One way to think of the Hamiltonian is that it encodes ‘the machinery of the world’ we are modeling.

Armed with both our wavefunction (list of 2ᴺ probability amplitudes) and our Hamiltonian (matrix of size 2ᴺx2ᴺ) we have everything we need to understand the Schrödinger Equation.

Here it is!!!

or equivalently, if we plug in the decomposition of the wavefunction over all the possible states of the system,

which is a system of 2ᴺ⁺¹ equations for the 2ᴺ⁺¹ unknowns aⱼ(t) (the plus one in the exponent comes from aⱼ(t) being complex, so it’s actually two terms, the real and the imaginary part). We can solve this using standard numerical differential equation solvers, as long as N isn’t too big (the number of equations grows exponentially with N which limits exact solutions to fairly small quantum systems!).

The Schrödinger Equation is a differential equation (it has derivatives — the d|Ψ(t)>/dt term means ‘the rate of change of |Ψ(t)> in time’) which tells us how the wavefunction changes with time due to the effects of the Hamiltonian. It introduces a new constant ħ, called Planck’s constant. i here is the square root of -1.

Remember that the wavefunction tells us what the probabilities are of measuring the system in all its potential states. This equation tells us that those probabilities can and do change over time, and it’s this Hamiltonian thing that ‘guides’ the wavefunction during its evolution.

In words, the equation says ‘the rate of change of the wavefunction, multiplied by iħ, is the wavefunction multiplied by the Hamiltonian’. That’s really most of what quantum mechanics is! If you’ve made it this far, congratulations, now you know 95% of what a physics undergrad knows.

With just this equation we can (in principle anyway, in practice is a different story) model most of the things we care about in the physical world.

What Building a Quantum Computer Means

To build a quantum computer, we need to construct an exquisitely engineered physical system that is described by some desired Hamiltonian. The Hamiltonian guides the changes in probabilities of measuring our qubits in some state | j >, which recall is just the binary number you get from measuring all of the N objects’ states.

Which Hamiltonian we choose depends on which model of computation we want to enable.

All models of quantum computation, including the gate or circuit model, work in the same way. A user programs the parameters of a Hamiltonian such that the evolution of the system in time (under the Schrödinger Equation) evolves the probabilities of being in all of the states | j >, where the more likely states hold information we are seeking to extract from the computation. For example the binary number 1001 might be a number that breaks a code, so if we run the quantum computation and read out the state | +1, -1, -1, +1 > at the end, we’ve found the key!

There is a lot of misunderstanding around what models of quantum computation imply. Largely for sociological reasons, the gate model of quantum computing is sometimes associated with ‘real’ quantum computing, which, as physicists are fond of saying, is not even wrong.

Any system described by a Hamiltonian whose evolution is governed by the Schrödinger Equation is by definition performing a quantum computation. (Whether this computation is useful is a separate question — but no quantum computer ever built clearly meets this standard… at least yet :-) ).

OK. Let’s assume that we’ve been skillful enough to engineer a physical system with some Hamiltonian H(t) which implements some model of computation.

The Schrödinger Equation then describes how the wavefunction of the system evolves in time under that Hamiltonian, and if you did a good job, when you measure the physical system at the end of the computation, you sample from the probability distribution defined by | Ψ(t) >, giving state | j > with probability |aⱼ(t)|².

The D-Wave Approach to Building Quantum Computers

The D-Wave approach to quantum computation implements the following Hamiltonian, where the hⱼ and Jᵢⱼ terms are real numbers set in software (ie they are fully programmable):

Here tₐ is the computation time in units of time (typically around tₐ = 5 nanoseconds), s is a dimensionless time that changes from s=0 to s=1 over a computation (note: this has nothing to do with our previous use of s to denote two state variables, this is a totally different s which runs from 0 to 1 over the course of a computation), N is the number of qubits (can be up to the number of qubits in a D-Wave chip, which for the Advantage2 system we’ll be using is 576), 𝝙(s) and 𝚪(s) are fixed hardware-specific envelope functions with units of energy (the Advantage2 fast anneal ones are shown in the figure below), σˣⱼ and σᶻⱼ are the Pauli x and z matrices respectively for qubit j, E is the set of couplers between qubits in a chip (not all qubits are physically connected to all others, there are about 10,000 total connections in Advantage2), hⱼ is the dimensionless bias on qubit j, and Jᵢⱼ is the dimensionless coupling between qubits i and j.

The Advantage2_prototype2.3 fast annealing schedule for the D-Wave Advantage2.3 system. You can find the data files for these terms here.

𝝙(s) and 𝚪(s) are engineered so that at the beginning of a computation (near s=0), the first term in the Hamiltonian (the one with the σˣ terms) dominates. In this limit, the system is in an equal superposition of all possible 2ᴺ states, and if we measure the qubits, we’ll get all the possible 2ᴺ outcomes with equal probability (p=1/2ᴺ). If we interpret the qubits as being quantum magnets (with the physical device creating magnetic fields that point up or down depending on the state of the qubit, which is literally true in the D-Wave approach), the system in the s=0 limit is a paramagnet.

As a computation proceeds towards s=1, the first term vanishes and the second term (with the σᶻ terms) picks up and eventually dominates. The process of driving from s=0 to s=1 is called quantum annealing. The system in the s=1 limit, for suitable choices of hⱼ and Jᵢⱼ, again interpreting the qubits as quantum magnets, is a spin glass.

The D-Wave computational paradigm drives the system from paramagnet to spin glass through a quantum phase transition. An example of a phase transition is when liquid water freezes — ice is still water but in a different (solid vs liquid) phase. Quantum phase transitions are the same, except to model them we need to treat the system quantum mechanically.

If you drive the computation fast enough, it’s called a quantum quench. This is the regime we will always be in for our work. A quench is when you drive a physical system through a phase transition very quickly. This is what happens when, for example, a blacksmith puts a red hot sword blade directly into cold water or oil. The quenching process ‘freezes in’ defects in the material that can give it desirable properties. When you quench a quantum magnet, you also get the same effect!

Here’s a cool video showing what a quench looks like for metal. When we run a D-Wave system fast, there’s a similar thing going on, but what’s being quenched isn’t temperature, but the thing that allows for the qubits to tunnel between their two states.

After a computation is done (at time s=1), the state of all N qubits are read out as a list of +1 and -1 variables. This which samples from the probability distribution defined by

returning the N variable binary state | j > with probability |aⱼ(s=1)|². Because the computation time in a D-Wave machine in the quantum quench regime is so fast (the time to perform one of these computations is tₐ which is about 5 nanoseconds) we can and usually do repeat these measurements many times. If we draw M samples from the probability distribution defined by the system’s wavefunction at the end of the computation, it takes about 5*M nanoseconds to do so.

The computation I’ve described here is in a category of quantum computing algorithms called quantum simulation algorithms, where a quantum computer is used to simulate another quantum system. In this case, it’s the simulation of the final state of a quantum magnet after being quenched through the quantum phase transition between paramagnetic and spin glass states.

The D-Wave Approach Draws Samples From A Probability Distribution Over an Ising Model

At s=1, once the computation is done, the Hamiltonian of the system is dominated by the second term. This second term is an Ising model. This means that when we measure the states of the qubits, we are drawing samples from a probability distribution whose energies are the Ising model energies. The energy of any measured state | j > in the D-Wave processor is

where the gamma thing has units of energy and whose value is around 6 GHz in units where ℏ=1. If the system is in thermal equilibrium at some temperature T, the probability distribution given by the wavefunction |Ψ(s=1)> would have Boltzmann statistics, exactly like we talked about in a previous post, and we’d know what all the probabilities should be by just plugging them into the Boltzmann distribution.

However in this case, in general |Ψ(s=1)> is not Boltzmann!!! If the computation is fast enough, the system does not have time to thermally equilibrate, and when we measure the qubits at s=1 they do not have to be, and generally aren’t, in thermal equilibrium.

If the Hamiltonian I wrote down is the actual Hamiltonian of the quantum computer, the actual probability distribution in reality is given by |Ψ(s=1)>, and there’s no simple way to generate such a distribution using non-quantum computers, and therefore no simple way to figure out what the samples we measure are going to be, without actually running the quantum computation described above.

This is the basis for the quantum supremacy claim D-Wave made in this paper. Their claim is that it is not feasible to compute |Ψ(s=1)> for large enough systems using any classical computer and therefore the samples that they draw can’t be predicted using any classical computer.

Computing Correlation and Influence From Samples From a D-Wave Quantum Computation

If we run M computations (and thereby draw M samples from |Ψ(s=1)>), each of these samples returns N +1 or -1 values. For example if we have N=4 qubits, and we draw M=3 samples, we might see [+1,+1,-1,-1], [+1,+1,+1,-1], and [-1,+1,-1,-1].

These samples are just like the coin tosses we talked about earlier — each is a just a list of N +1 or -1 values, like heads or tails from a coin toss.

We can then easily compute the N*(N-1)/2 pairwise correlations between each variable over this set of samples, and then compute the influence of each variable.

If it’s true that |Ψ(s=1)> after a quantum quench through the quantum phase transition between paramagnetic and spin glass phases can only be computed by a D-Wave quantum computer, then computing the correlations, and then the influence of each variable for particular settings of h and J, are domains of quantum supremacy, and no possible classical computer could ever compute them!

Quantum Mechanics and Quantum Computers